VECTORES Y MRU

  movimiento rectilíneo uniforme

Un movimiento es rectilíneo cuando un móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU, que en algunos países es MRC, que significa Movimiento Rectilíneo Constante.

¿QUE ES MOVIMIENTO RECTILÍNEO UNIFORME?

El movimiento rectilíneo uniforme (MRU) fue definido, por primera vez, por Galileo en los siguientes términos: "Por movimiento igual o uniforme entiendo aquél en el que los espacios recorridos por un móvil en tiempos iguales, tómese como se tomen, resultan iguales entre sí", o, dicho de otro modo, es un movimiento de velocidad v constante.

El MRU se caracteriza por:a) Movimiento que se realiza en una sola dirección en el eje horizontal.
b) Velocidad constante; implica magnitud, sentido y dirección inalterables.c) La magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración = 0).

Concepto de rapidez y de velocidad

Muy fáciles de confundir, son usados  a menudo como equivalen tes para referirse a uno u otro.Pero la rapidez (r) representa un valor numérico, una magnitud; por ejemplo, 30 km/h.En cambio la velocidad representa un vector que incluye un valor numérico (30 Km/h) y que además posee un sentido y una dirección.Cuando hablemos de rapidez habrá dos elementos muy importantes que considerar: la distancia (d) y el tiempo (t), íntimamente relacionados.Así:Si dos móviles demoran el mismo tiempo en recorrer distancias distintas, tiene mayor rapidez aquel que recorre la mayor de ellas.Si dos móviles recorren la misma distancia en tiempos distintos, tiene mayor rapidez aquel que lo hace en menor tiempo.

Significado físico de la rapidezLa rapidez se calcula o se expresa en relación a la distancia recorrida en cierta unidad de tiempo y su fórmula general es la siguiente:                                                   

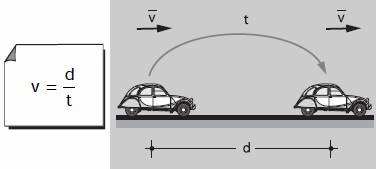Donde v = rapidez         d = distancia o desplazamiento    t = tiempo

 Usamos v para representar la rapidez, la cual es igual al cociente entre la distancia (d) recorrida y el tiempo (t) empleado para hacerlo.Como corolario, la distancia estará dada por la fórmula:                                                      
                                                          

Según esta, la distancia recorrida por un móvil se obtiene de multiplicar su rapidez por el tiempo empleado.A su vez, si se quiere calcular el tiempo empleado en recorrer cierta distancia usamos                                                              

El tiempo está dado por el cociente entre la distancia recorrida y la rapidez con que se hace.


EJERCICIOS DE MRU:

EJERCICIO 1:dos automóviles   parten desde un mismo punto, con movimiento rectilíneo uniforme. un móvil amarillo (móvil A) se desplaza hacia el norte a 90 km por hora, y otro rojo (móvil B), hacia el sur a 80 km por hora. Calcular la distancia que los separa al cabo de 2 horas.Veamos los datos que tenemos:
Para el móvil A:


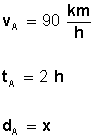
Para el móvil B:

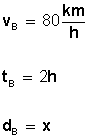
Calculamos la distancia que recorre el móvil A:

Calculamos la distancia que recorre el móvil B:

Sumamos ambas distancias y nos da 340 km como la distancia que separa a ambos automóviles luego de 2 horas de marcha.


EJERCICIO 2:un carro se desplaza con movimiento rectilíneo uniforme ¿cuánto demorará en recorrer 258 kilómetros si se mueve con una rapidez de  86 kilómetros por hora?
Analicemos los datos que nos dan:

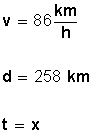
Apliquemos la fórmula conocida para calcular el tiempo:
 y reemplacemos con los datos que tenemos:

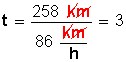
¿Qué hicimos? Para calcular el tiempo (t), valor desconocido, dividimos la distancia (d) por la rapidez (v),  simplificamos la unidad kilómetros y nos queda el resultado final en horas: 3 horas para recorrer 258 km  con una rapidez de 86 km a la hora.


EJERCICIO 3:un corredor  trota de un extremo a otro de la pista en línea recta 300 m en 2,5 min., luego se devuelve y trota 100 m hacia el punto de partida en otro minuto.
Preguntas: ¿Cuál es la rapidez promedio del atleta al recorrer  ambas distancias? ¿Cuál es la rapidez media del atleta al recorrer los 400 metros?
Veamos los datos que tenemos:
Para el primer tramo:

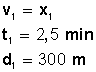
Calculamos su rapidez:

Para el segundo tramo:
Calculamos su rapidez:

Rapidez promedio:

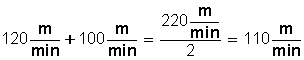
La rapidez promedio del atleta fue de 110 metros por minuto.
Veamos ahora cuál fue la velocidad media (v_m)para recorrer los 400 metros
La rapidez media del atleta fue de 114,29 metros por minuto.

                                                   VECTORESEn física, un vector  es una magnitud física definida por un punto del espacio donde se mide dicha magnitud, además de un módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).DEFINICIÓN DE VECTORES:
Se llama vector de dimensión  a una tupla de  números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión  se representa como  (formado mediante el producto cartesiano).
Así, un vector  perteneciente a un espacio  se representa como:
, donde 
 CARACTERÍSTICAS DEL VECTOR:
Si representamos el vector gráficamente podemos diferenciar la recta soporte o dirección, sobre la que se traza el vector.
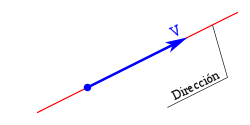El módulo o amplitud con una longitud proporcional al valor del vector.
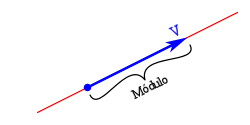El sentido, indicado por la punta de flecha, siendo uno de los dos posibles sobre la recta soporte.
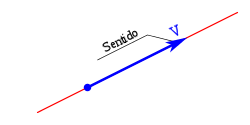El punto de aplicación que corresponde al lugar geométrico al cual corresponde la característica vectorial representado por el vector.
El nombre o denominación es la letra, signo o secuencia de signos que define al vector.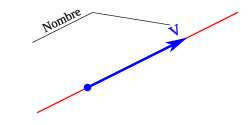
Por lo tanto en un vector podemos diferenciar:
Nombre
Dirección
Sentido
Módulo
Punto de aplicación


TIPOS DE VECTORES:

—1.- Fijos o ligados :Llamados también vectores de posición. Son aquellos que tienen un origen fijo .Fijan la posición de un cuerpo o representan una fuerza en el espacio.










.-Vectores deslizantes : Son aquellos que pueden cambiar de posición a lo largo de su directriz.
—Ejemplo.










—3.- Vectores libres: Son aquellos vectores que se pueden desplazar libremente a lo largo de sus direcciones o hacia rectas paralelas sin sufrir modificaciones.










4.- Vectores paralelos: Dos vectores son paralelos si las rectas que las contienen son paralelas.
Ejemplo.










5.-Vectores coplanares: Cuando las rectas que lo contienen están en un mismo plano.
Ejemplo.










6.-Vectores concurrentes: Cuando sus líneas de acción o directrices se cortan en un punto.
Ejemplo.








7.-Vectores colineales: Cuando sus líneas de acción se encuentran sobre una misma recta.Ejemplo.




MAGNITUDES VECTORIALES:Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.
Masa
Temperatura
Presión
Densidad

Magnitudes Escalares

Denominamos Magnitudes Escalares a aquellas en las que las medidas quedan correctamente expresadas por medio de un número y la correspondiente unidad. Ejemplo de ello son las siguientes magnitudes, entre otras:

EJERCICIOS DE VECTORES:

EJERCICIO 1:

 Dado el vector = (2, −1), determinar dos vectores equipolentes a , , sabiendo que A(1, −3) y D(2, 0).

SOLUCION:

EJERCICIO 2:
Dados los vértices de un triángulo A(1, 2), B(−3, 4) y C(−1, 3), hallar las coordenadas del baricentro.

SOLUCIÓN:

 


EJERCICIO 3:
Hallar las coordenadas del punto C, sabiendo que B(2, −2) es el punto medio de AC, A(−3, 1).

SOLUCIÓN: